Międzynarodowy zespół naukowców wykazał, że ciąg Fibonacciego może kierować topologicznym transportem światła w materiałach quasi-okresowych, łamiąc zasadę ścisłej okresowości.
Liczby ciągu Fibonacciego występują w spiralach muszli, układzie płatków wielu kwiatów i strukturze niektórych galaktyk. Ich powtarzające się występowanie w zjawiskach naturalnych sprawiło, że ta sekwencja matematyczna stała się symbolem harmonii. Teraz międzynarodowy zespół naukowców znalazł dla niej nowe zastosowanie:kontrolowany i stabilny transport światła przez materiały zaprojektowane specjalnie do tego celu.
W badaniu opublikowanym w czasopiśmie eLight fizycy pod kierownictwem Fangwei Ye z Uniwersytetu Jiao Tong w Szanghaju wraz z kolegami z Portugalii i Rosji wykazali eksperymentalnie, że możliwe jest kontrolowane „pompowanie” światła zgodnie z wzorami określonymi przez ciąg Fibonacciego. Praca opiera się na koncepcji fizyki znanej jako pompowanie topologiczne, która wykorzystuje globalne właściwości systemu do precyzyjnego i odpornego na zakłócenia przenoszenia energii lub cząstek. Nowością jest to, że pompowanie nie odbywało się w środowisku okresowym, jak dotychczas, ale w środowisku quasiokresowym, co łamie zasadę uważaną za fundamentalną.

Od Nagrody Nobla do nowego paradygmatu optycznego
Pompowanie topologiczne zostało zaproponowane w 1983 roku przez noblistę Davida J. Thoulessa w celu wyjaśnienia, w jaki sposób elektrony mogą przemieszczać się w kontrolowany sposób w potencjale okresowym modulowanym w czasie. Mechanizm ten charakteryzuje się zależnością od niezmiennej topologicznej — liczby Cherna — oraz odpornością na lokalne defekty środowiska. Według artykułu jest to zjawisko „niewrażliwe na lokalne niedoskonałości środowiska” i mające zastosowanie w wielu dziedzinach, od optyki po akustykę.
Dotychczas badania koncentrowały się na układach, w których modulacja czasowa była ściśle okresowa, co gwarantowało powtarzalność stanu układu w określonych odstępach czasu. Nowa praca stawia ambitne pytanie: czy możliwe jest utrzymanie pompowania topologicznego, jeśli ta idealna okresowość zostanie zakłócona? Zespół zbadał konfigurację quasi-okresową, modulując układ za pomocą dwóch częstotliwości, których iloraz jest liczbą nieracjonalną. W tym przypadku wybrano złoty podział, ściśle powiązany z ciągiem Fibonacciego.
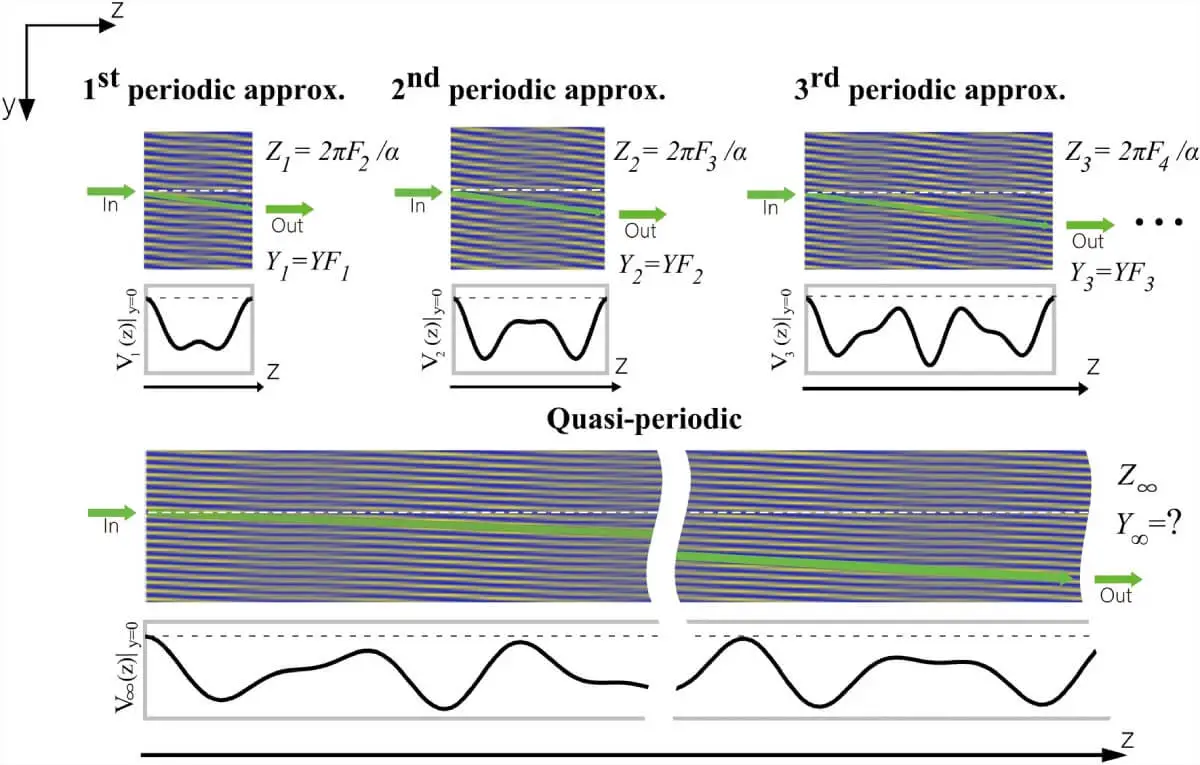
Zdjęcie pokazuje, jak światło przemieszcza się w sieciach quasi-okresowych przy użyciu aproksymacji okresowych, ujawniając pompowanie optyczne i trajektorię wiązki w ciągu jednego cyklu.
Jak Fibonacci łączy się z ruchem światła
Autorzy przypominają, że każdą liczbę nieracjonalną można przybliżyć za pomocą ułamków złożonych z liczb całkowitych. W przypadku liczby złotej ułamki te uzyskuje się bezpośrednio z ciągu Fibonacciego, gdzie każdy wyraz jest sumą dwóch poprzednich. W ten sposób stosunek między dwiema częstotliwościami modulacji można stopniowo przybliżać za pomocą stosunków takich jak 1/2, 2/3, 3/5, 5/8 i tak dalej.
W ich eksperymencie przełożyło się to na serię „okresowych aproksymant”, które naśladują zachowanie rzeczywistego systemu quasiokresowego. Aproksymanty te pozwoliły zastosować teoretyczne narzędzia konwencjonalnego pompowania topologicznego do przypadku, który w zasadzie nie spełnia jego zasad. Kluczowym odkryciem było to, że liczby Cherna obliczone dla każdego aproksymatora dokładnie odpowiadały ciągowi Fibonacciego: 1, 2, 3, 5, 8, 13… Jak zauważają, „liczba Cherna dla kolejnych aproksymatorów pokrywa się z liczbami Fibonacciego”, co bezpośrednio determinuje prędkość, z jaką przemieszcza się światło.
Konstrukcja optyczna do przetestowania teorii
Zespół pracował z fotorefrakcyjnym kryształem niobianu strontu i baru (SBN) o wymiarach 5×5×20 mm³. Wykorzystali technikę zwaną indukcją optyczną, w której zwykłe spolaryzowane wiązki laserowe interferują, tworząc wzór refrakcji wewnątrz kryształu. Wzór ten działa jak „sieć”, która kieruje wiązkę testową, w tym przypadku niezwykle spolaryzowaną, wzdłuż osi podłużnej.
Każde zbliżające się okresowe zbliżenie wymagało nieco innego wzoru, z okresami podłużnymi powiązanymi zgodnie z liczbami Fibonacciego. W praktyce długość kryształu pozwoliła na wykonanie tylko trzech pierwszych zbliżeń, o długościach półfazy odpowiednio 8, 12 i 19 mm. We wszystkich przypadkach zespół zmierzył boczne przesunięcie środka ciężkości wiązki po przejściu połowy cyklu pompowania.
Wyniki: ślad Fibonacciego w przesunięciu
Pomiary eksperymentalne wykazały przesunięcie wiązki zgodne z przewidywaniami teoretycznymi dla każdego aproksymatora, zgodnie z regułą Fibonacciego. Nawet przy znacznych zmianach amplitudy sieci spowodowanych zmianami napięcia prędkość pompowania pozostała praktycznie stała. Potwierdza to, że topologiczna odporność utrzymuje się w reżimie quasi-okresowym.
Artykuł wyjaśnia, że „prędkość pompowania jest określana przez globalne właściwości topologiczne pasm”, a nie przez lokalne niedoskonałości lub nieuporządkowanie. Ponadto symulacje numeryczne odtworzyły zaobserwowane zachowanie, w tym zbieżność średniej prędkości do wartości granicznej określonej przez złoty podział.

Co to oznacza dla fizyki i technologii
Praca ta pokazuje, że nie jest konieczna ścisła okresowość czasowa, aby uzyskać pompowanie topologiczne, co znacznie rozszerza możliwości projektowania systemów fotonicznych i innych mediów falowych. Strategia wykorzystania aproksymacji okresowych do opisu systemu quasi-okresowego otwiera również drzwi do zbadania innych liczb nieracjonalnych niż złoty.
Autorzy sugerują, że koncepcja ta może znaleźć zastosowanie w takich dziedzinach, jak atomy ultra-zimne, plazmonika lub systemy akustyczne, gdzie można wdrożyć modulacje quasi-okresowe. Wskazują również, że wykorzystana platforma eksperymentalna pozwala badać interakcje między topologią, symetrią i nieliniowością, co może potencjalnie doprowadzić do odkrycia nowych stanów materii i zaprojektowania urządzeń kwantowych o unikalnych właściwościach transportowych.
Wyzwania i kierunki dalszych badań
Pomimo sukcesu, eksperymenty napotkały poważne wyzwanie: dyfrakcję wiązki podczas pompowania, która nasila się w przypadku aproksymacji wyższych rzędów. Zmniejszenie tego efektu wymagałoby zwiększenia głębokości sieci, co jest ograniczone techniką indukcji optycznej. Wśród możliwych rozwiązań można wymienić zastosowanie układów dyskretnych falowodów, które umożliwiają większe ograniczenie, lub wykorzystanie efektów nieliniowych w celu utrzymania lokalizacji wiązki.
Innym kierunkiem badań będzie przeniesienie tego quasi-okresowego pompowania do układów dwuwymiarowych, takich jak sieci fotoniczne typu moiré, gdzie dyfrakcja może być lepiej kontrolowana. Tego typu konfiguracje mogą ujawnić jeszcze bardziej złożone i odporne zachowania transportowe.

Poza optyką
Wykazanie, że ciąg Fibonacciego może kierować transportem światła, nie jest tylko ciekawym odkryciem: jest to dowód, że prawa matematyczne rządzące naturą mogą być wykorzystane do kontrolowania ruchu energii w sposób przewidywalny i odporny. Fakt, że wzór numeryczny występujący w kwiatach i galaktykach może znaleźć zastosowanie w technologiach manipulacji światłem, ilustruje głęboki związek między matematyką a fizyką eksperymentalną.Jak podsumowują autorzy, strategia zbliżania systemu quasi-okresowego za pomocą sekwencji okresowych „pozwala zaobserwować stosunkowo szybkie przejście do średniej prędkości pompowania, potwierdzając jego topologiczne pochodzenie”. Innymi słowy, światło podlega regułom Fibonacciego nawet w środowisku, które łamie klasyczne zasady pompowania topologicznego.








